La bilancetta
Forse non tutti sanno che Galileo era un appassionato lettore delle opere di Archimede, [1] e che nella sua prima opera scientifica in volgare "La bilancetta", [2] descrive un metodo alternativo a quello visto nella prima parte di questo articolo per risolvere il problema della corona.
Ma perché Galileo non era convinto della versione data da Vitruvio? Le obiezioni mosse sono due. La prima è di tipo qualitativo:
"par cosa, per così dirla, molto grossa e lontana dall'esquisitezza"
il ragionamento alla base del procedimento gli sembra troppo elementare. È quasi grottesco pensare che per un fatto tanto banale, come quello per cui immergendo un corpo in una vasca il livello dell'acqua al suo interno sale, il matematico si sia lanciato nudo per le strade di Siracusa gridando Eureka! Come invece sembra voler far credere Vitruvio.
Persino i corvi, come potete vedere, hanno un'ottima padronanza del concetto. [3]

Un corvo è in grado di sfruttare lo stesso principio per procurarsi del cibo.
La seconda è invece di tipo quantitativo e non lascia scampo:
"tal modo era in tutto fallace e privo di quella esattezza che si richiede nelle cose matematiche"
Galileo aveva capito che i volumi d'acqua che Archimede avrebbe dovuto misurare erano semplicemente troppo piccoli per il metodo di misurazione scelto.
Facciamo qualche calcolo
Per prima cosa cerchiamo di capire come erano fatte le corone votive dell'epoca. Rifacendoci ai reperti recuperati dagli archeologi sappiamo che nessuna di queste superava il kilogrammo.

esempio di corona votiva greca conservata al Museo archeologico di Thessaloniki.
Prendendo come esempio quella ritrovata nella tomba di un altro re, ipotizziamo per la corona una massa di 700 grammi. [4]
...
Noti i valori delle densità di oro e argento
... ...
possiamo ricavare i volumi dei blocchi utilizzati da Archimede nel racconto di Vitruvio:
...
...
se li immaginiamo di forma sferica, quello d'oro avrà le stesse dimensioni di una pallina da ping pong, mentre quella d'argento sarà di poco più grande.
...
L'aumento del livello dell'acqua causato dall'immersione di questi volumi in una vasca di dimensioni appena sufficienti per immergere la corona, che ipotizziamo abbia un'imboccatura quadrata di lato l = 32 cm, sarà dato da:
...
...
anche ipotizzando una vasca diversa, più alta e stretta, con una imboccatura rettangolare (32 cm x 10 cm) il dislivello sarebbe comunque nell'ordine del mm. [5]
Dunque è evidente che il metodo per la misurazione dei volumi per immersione non è abbastanza sensibile per distinguere con la dovuta precisione i valori dei tre volumi coinvolti nel ragionamento.
il principio di Archimede
Galileo, dopo aver esposto i suoi dubbi, prosegue dicendo:
mi è venuto in mente un modo che esquisitissimamente risolve il nostro quesito: il qual modo crederò io esser l'istesso che usasse Archimede, atteso che, oltre all'esser esattissimo, dipende ancora da dimostrazioni ritrovate dal medesimo Archimede
In particolare la dimostrazione che sfrutterà è la seguente:
"un solido più pesante di un fluido, se collocato in esso, discenderà in fondo al fluido e se si peserà il solido nel fluido, risulterà più leggero del suo vero peso, e la differenza sarà uguale al peso del fluido spostato". [6]
[Archimede - "Galleggianti" Lib. I, Proposizione 7]
caso particolare dell'enunciato più generale, oggi conosciuto proprio come principio di Archimede:
"un corpo immerso in un fluido riceve una spinta verso l'alto pari al peso del volume del fluido spostato"
In termini quantitativi tale forza può essere espressa, utilizzando la definizione del peso di un corpo come il prodotto della massa per l'accelerazione gravitazionale g:
...
... (valore medio sulla superficie terrestre)
e della densità di un corpo con la formula:
...
il metodo di Galileo
Il procedimento ideato da Galileo si basa sul principio di Archimede e prevede l'utilizzo di una bilancia a due bracci, [7] come quella qui raffigurata, che utilizzeremo come riferimento durante la spiegazione:
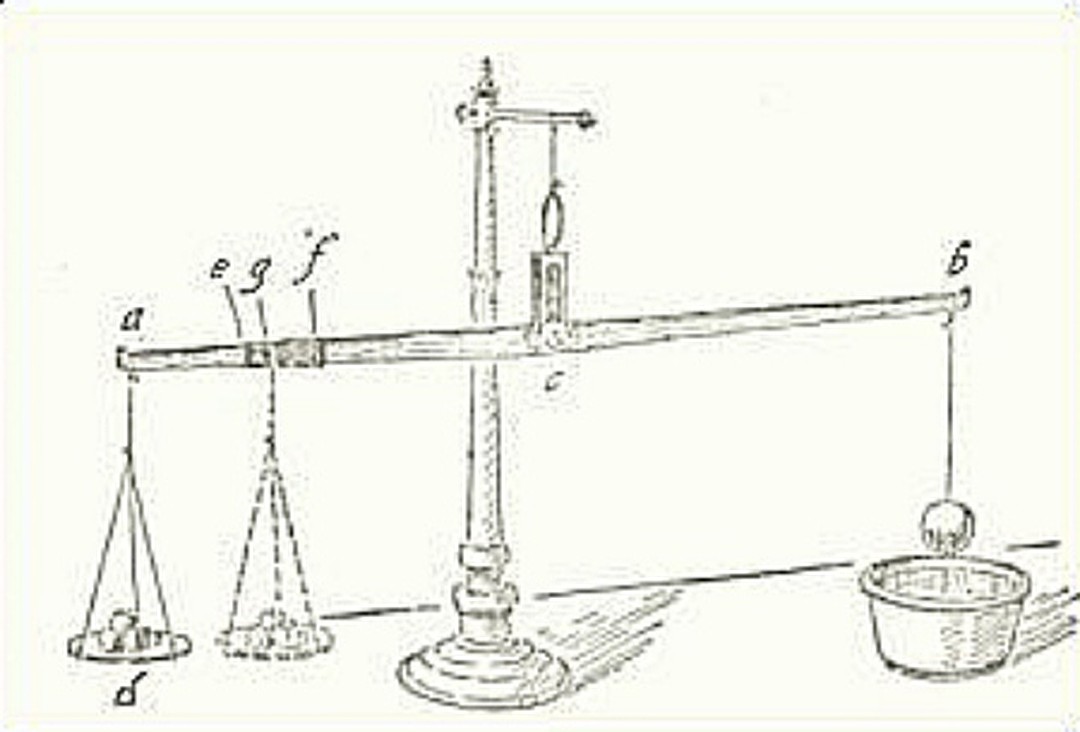
Illustrazione della bilancetta idrostatica di Galileo
per prima cosa si procede alla pesatura in aria dei due blocchi di argento e oro. Nell'ipotesi che abbiano la stessa massa, applicati all'estremo b, essi saranno bilanciati dallo stesso identico contrappeso d posto all'estremo a della bilancia. La condizione di equilibrio vuole che i prodotti delle due forze per la distanza dal fulcro del loro punto di applicazione siano uguali:
...
se le due masse sono uguali avranno lo stesso peso, quindi per la condizione di equilibrio avremo:
...
Ora se si immerge il blocco di metallo in acqua, per effetto del principio di Archimede, la forza agente su b diminuirà di un valore proporzionale al volume del corpo immerso, determinando così la rottura dell'equilibrio iniziale e facendo pendere la bilancia dalla parte del contrappeso.
Per riottenere l'equilibrio dovremo avvicinare il contrappeso al fulcro c della bilancia, fino a trovare il punto, (e nel caso dell'oro), per cui si avrà:
...
Dal momento che il volume occupato dall'argento è maggiore di quello occupato dall'oro, la spinta di Archimede sarà maggiore nel primo caso, e pertanto per ristabilire l'equilibrio della bilancia si dovrà spostare il contrappeso ancora più vicino al fulcro. (punto f dell'illustrazione).
Nel caso di una corona contraffatta l'equilibrio verrà ristabilito in un punto g compreso tra quelli individuati per i blocchi di metallo puro (e, f) e la frazione d'argento sarà data:
"dalla proporzione nella quale verrà divisa la distanza EF si averà esquisitamente la proporzione dei due metalli, che tal misto compongono."
e nel dettaglio:
l'oro e l'argento, che compongono tal misto, sono tra di loro nella medesima proporzione che le distanze FG, GE. Ma ci è da avvertire che la distanza GF, terminata nel segno dell'argento, ci denoterà la quantità dell'oro, e la distanza GE, terminata nel segno dell'oro, ci dimostrerà la quantità dell'argento: di maniera che se FG tornerà doppia di GE, il tal misto sarà due d'oro ed uno di argento. E col medesimo ordine procedendo nell'esamine di altri misti, si troverà esquisitamente la quantità dei semplici metalli.
Quanto è preciso?
Galileo conclude l'opera dando istruzioni dettagliate su come costruire la bilancia. E indica subito al lettore su quale parte intervenire per migliorarne la sensibilità:
Per fabricar dunque la bilancia, piglisi un regolo lungo almeno due braccia, e quanto più sarà lungo più sarà esatto l'istrumento
Proviamo a stimare la sensibilità della bilancia ipotizzando che ciascun braccio sia lungo 60 cm, [8] e riutilizzando i valori dei volumi dei blocchi di metallo ricavati nell'ipotesi di una corona di massa 0,7 kg. La forza peso in aria iniziale sarà uguale per tutte le masse in gioco:
...
il valore della spinta di Archimede dipenderà invece dai volumi dei blocchi, già calcolati, e dalla densità dell'acqua in cui li immergiamo:
... (alla temperatura di 22° C)
...
...
...
...
imponendo la condizione di equilibrio ricavo i segmenti EC e FC:
...
...
ponendo uguale a x la frazione di argento, possiamo scrivere la Forza di Archimede agente sulla corona:
...
ipotizzando che la sensibilità nel misurare le lunghezze fosse di 4 mm, tenendo conto dello spessore dei fili, con una bilancia come questa si potrebbero rilevare frazioni d'argento pari a: [9]
...
Come detto, utilizzando una bilancia con bracci di lunghezza maggiore la frazione minima di argento rilevabile dallo strumento diminuirà senza dover migliorare la sensibilità nella misura delle lunghezze.
Note
| [1] | nei "Discorsi e dimostrazioni matematiche intorno a due nuove scienze", [Giornata I, 86], pubblicato a Leida nel 1638, ribadisce la sua stima nei confronti dell'illustre predecessore, quando fa dire a Salviati: "mi rese credibile ogni miracolo, che si legge in più scrittori, la lettura de i libri dell'istesso Archimede, già da me con infinito stupore letti e studiati". |
| [2] | scritta nel 1586, a soli 22 anni, in volgare anziché in latino, per ottenere la cattedra di matematica all'università di Pisa. |
| [3] |
senza offesa ovviamente ... 😰 Gli uccelli (The Birds), regia di Alfred Hitchcock, 1963 |
| [4] | nella tomba di Filippo II, padre di Alessandro Magno, ne è stata ritrovata una di 714 g. |
| [5] |
... ... |
| [6] | ho leggermente modificato la traduzione tratta dall'edizione UTET delle opere di Archimede per renderla più chiara. L'originale è qui riportato: "Le [grandezze] più pesanti del liquido, abbandonate nel liquido, sono trasportate verso il basso, fino al fondo, e saranno tanto più leggiere nel liquido, quanto è il peso del liquido avente tale volume quanto è il volume della grandezza solida." |
| [7] | Il plurale maschile bracci si usa quando indica oggetti o parti di oggetti che sporgono o si prolungano a somiglianza d’un braccio. esempi: "i bracci della croce, candelabro a sei bracci, i bracci di un edificio, ...". Il plurale femminile braccia si usa quando ci si riferisce agli arti superiori del corpo umano, in senso proprio o figurato. |
| [8] | Ipotizzando che l'unità di misura utilizzata da Galileo fosse il braccio fiorentino equivalente a 58,3 cm di oggi. |
| [9] |
la condizione da cui ho ricavato la x è la seguente: ... da cui ricavo ... ... ... ... |
| [9] |
| [3] |
| [5] |
Bibliografia
- Galileo Galilei, La bilancetta, 1586
- Frajese A., Opere di Archimede, UTET, 1974
- Boyer C.B., Storia della matematica, Mondadori, 2017
NOTA: i link a pagine esterne sono stati controllati l'ultima volta il 5 luglio 2018