Teoremi sui triangoli (qualsiasi)
"L'area di un triangolo è uguale alla metà del prodotto delle misure di due lati per il seno dell'angolo compreso"
Per dimostrare il teorema suddividiamo il triangolo scaleno ABC in due triangoli rettangoli AHC e HBC.
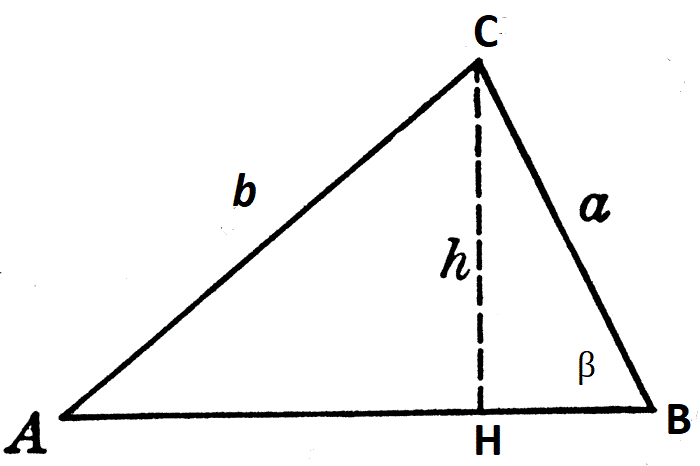
l'area del triangolo ABC sarà data dalla consueta formula base per altezza diviso due:
...
applicando il primo teorema della trigonometria per i triangoli rettangoli al triangolo HBC, posso riscrivere l'altezza CH in funzione dell'angolo β:
...
e ricavare così l'espressione dell'area che dimostra il teorema:
...
Dato che lo stesso ragionamento può essere fatto per tutte le coppie di lati adiacenti del triangolo consideriamo dimostrate tutte e tre le relazioni:
...
Teorema della corda
"La misura di una corda [1] di una circonferenza è uguale al prodotto della misura del diametro per il seno di uno qualunque degli angoli alla circonferenza [2] che insistono su uno dei due archi sottesi dalla corda."
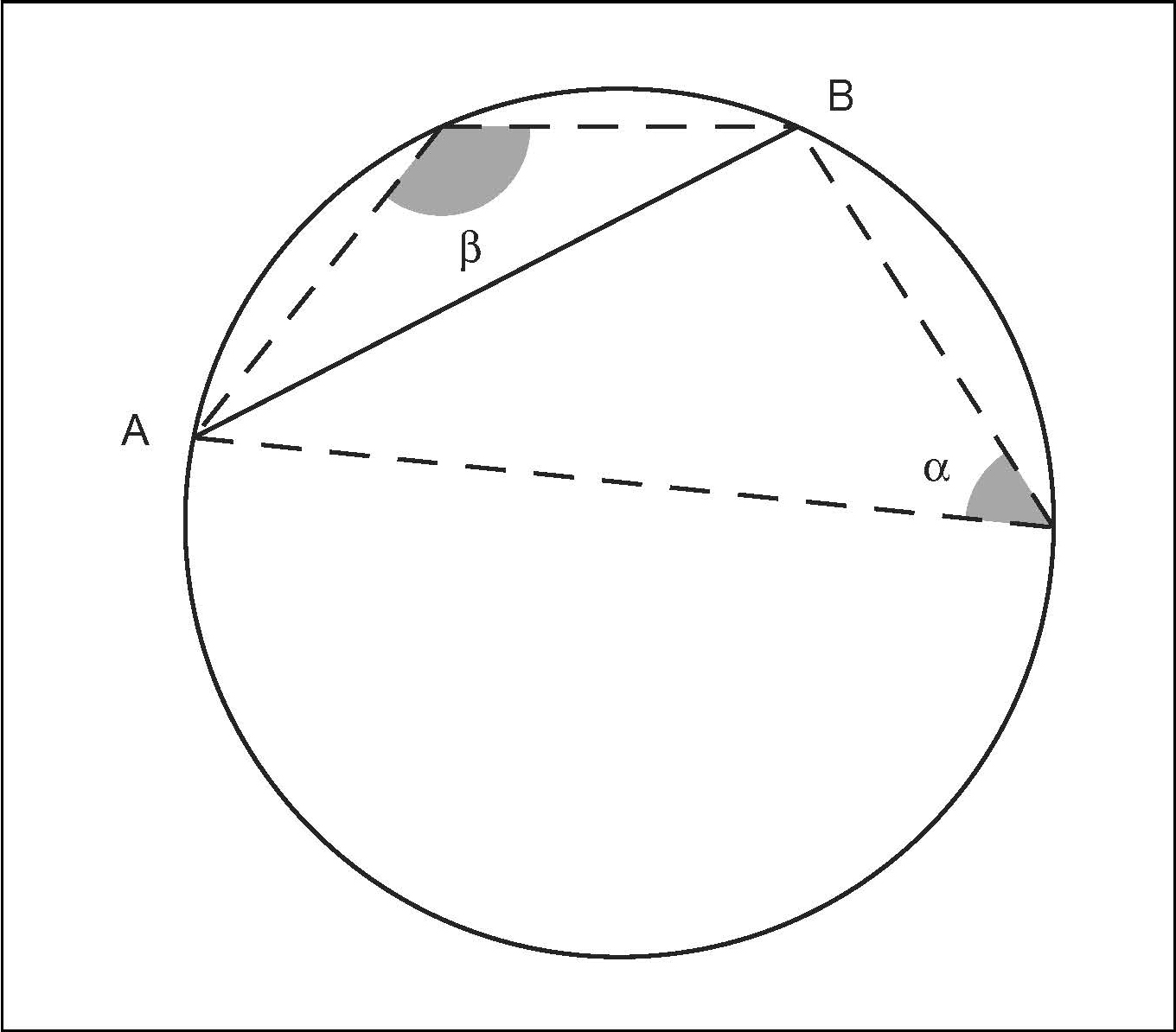
dato che la misura del diametro è uguale al doppio del raggio della circonferenza il teorema mi permette di scrivere:
...
Quando la corda coincide con un diametro, la dimostrazione del teorema segue dal fatto che ogni angolo alla circonferenza che insiste su una semicirconferenza è retto. [3] Come si può vedere dall'immagine:
In questo caso particolare il teorema ci darebbe la seguente identità:
...
Nel caso in cui la corda AB non coincida con il diametro posso sempre considerare il diametro AM e sfruttare il fatto che l'angolo MBA è retto.
Per quanto sappiamo sui teoremi relativi ai triangoli rettangoli il cateto AB del triangolo MBA può essere scritto in funzione della sua ipotenusa AM e dell'angolo AMB:
...
Ora se immagino di spostare M in un punto H qualsiasi sull'arco AB su cui si trova M, l'angolo AHB sarà uguale all'angolo AMB, dal momento che:
"tutti gli angoli alla circonferenza che insistono sullo stesso arco (o su archi congruenti) sono congruenti."
Quindi possiamo dedurre anche che:
...
il che dimostra il teorema. Per completezza dobbiamo dimostrare che la stessa relazione vale per un angolo alla circonferenza il cui vertice è sull'altro arco che insiste sulla corda AB. Scelto un punto I dal momento che
"gli angoli opposti di un qualsiasi quadrilatero inscritto in una circonferenza sono complementari"
se considero il quadrilatero inscritto HBIA avrò che:
...
E dal momento che vale la seguente relazione tra i seni:
...
Abbiamo dimostrato il teorema anche in questo caso.
Teorema dei seni
"In un triangolo è costante il rapporto fra la misura di ciascun lato e il seno dell'angolo opposto."
...
per dimostrare il teorema, basta considerare la circonferenza circoscritta al triangolo e applicare il teorema della corda.
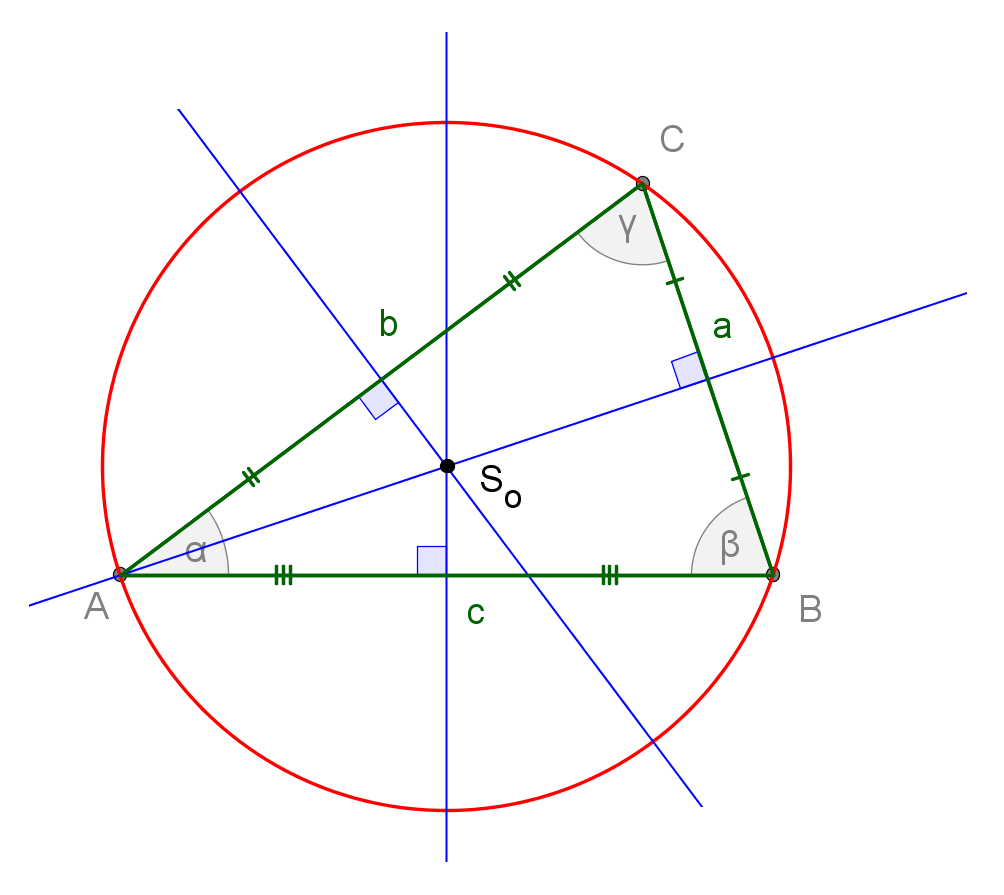
Così facendo ciascun lato coincide con una corda, la cui misura è data dal prodotto del diametro per il seno dell'angolo opposto:
...
...
...
possiamo quindi dedurre l'uguaglianza tra i rapporti:
...
Teorema del coseno
"In un triangolo il quadrato della misura di un lato è uguale alla somma dei quadrati delle misure degli altri due, diminuita del doppio prodotto delle misure di questi due lati per il coseno dell'angolo fra di essi compreso."
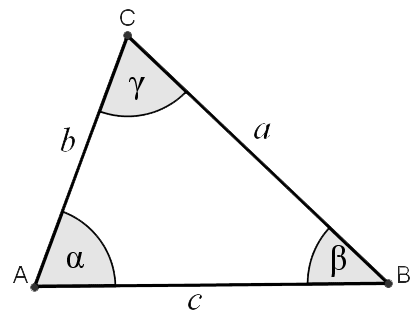
Questo teorema può essere considerato come una generalizzazione del teorema di Pitagora, che si ottiene da questo come caso particolare quando uno dei tre angoli misura 90°.
...
...
...
Note
| [1] | Si chiama corda ogni segmento che ha per estremi due qualsiasi punti di una circonferenza. Una corda che passa per il centro della circonferenza si chiama diametro. |
| [2] | Si chiama angolo alla circonferenza ogni angolo convesso che ha il vertice su una circonferenza e i due lati entrambi secanti la circonferenza, oppure uno secante e l'altro tangente alla circonferenza. |
| [3] | questo risultato è un corollario del teorema che lega tra loro la misura degli angoli al centro con quelli alla circonferenza: "ogni angolo alla circonferenza è la metà del corrispondente angolo al centro" |