la trigonometria è quella parte della matematica che tratta le relazioni tra le misure dei lati e le funzioni goniometriche degli angoli di un triangolo. La notazione standard utilizzata solitamente per indicare le varie parti del triangolo è la seguente:
- Le prime tre lettere maiuscole dell'alfabeto italiano A,B,C disposte dal vertice in basso a sinistra in senso antiorario indicano i vertici.
- Gli angoli di ciascun vertice sono indicati con la corrispondente lettera greca α,β,γ.
- I lati sono invece indicati con la lettera minuscola del vertice opposto a,b,c.
Triangoli rettangoli
Iniziamo considerando i triangoli rettangoli, ovvero quelli che hanno un angolo retto, ad esempio α = 90° = π/2 radianti.

Rappresentazione di un triangolo rettangolo
Dal momento che la somma degli angoli interni di ogni triangolo deve dare come somma 180° = π rad.
... (triangolo qualsiasi)
In un triangolo rettangolo la somma dei due angoli acuti β e γ deve per forza di cose essere 90°, quindi per definizione, β e γ sono angoli complementari.
... (triangolo rettangolo)
... (triangolo rettangolo)
per i triangoli rettangoli esiste una relazione che lega tra loro le misure dei tre lati: il teorema di Pitagora:
"In ogni triangolo rettangolo l'area del quadrato costruito sull'ipotenusa è uguale alla somma delle aree dei quadrati costruiti sui cateti."
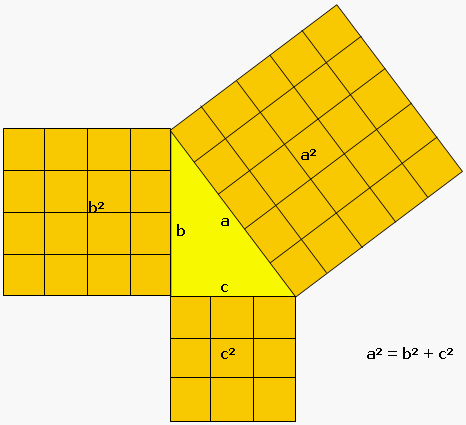
Rappresentazione del teorema di Pitagora
1° teorema sui triangoli rettangoli
"In un triangolo rettangolo la misura di un cateto è uguale a quella dell'ipotenusa moltiplicata per il seno dell'angolo opposto al cateto, o moltiplicata per il coseno dell'angolo acuto adiacente al cateto"
Questo teorema si può esprimere tramite le seguenti 4 formule:
...
...

2° teorema sui triangoli rettangoli
"In un triangolo rettangolo la misura di un cateto è uguale a quella dell'altro cateto moltiplicata per la tangente dell'angolo opposto al primo cateto, o moltiplicata per la cotangente dell'angolo acuto adiacente al primo cateto"
Questo risultato può essere ottenuto manipolando le formule del primo teorema e utilizzando le definizioni di tangente e cotangente qui riportate:
tan(α) = sin(α)/cos(α)
cotan(α) = 1/tan(α) = cos(α)/sin(α)
Dalle 4 relazioni del primo teorema possiamo ricavare la tangente di β:
... b = c tan(β)
e la cotangente di γ:
... b = c cot(γ)
da cui otteniamo le espressioni che esprimono il contenuto vero e proprio del teorema:
...
...
