il calcolo combinatorio

Disposizioni semplici

Sono sequenze in cui conta l'ordine degli elementi e nessun elemento può ripetersi. Per generare una sequenza di questo tipo possiamo prendere un sacchetto contenente 26 tessere, una per ciascuna lettera dell'alfabeto e generare la sequenza estraendo k tessere, con k minore o uguale di 26, senza rimettere nel sacchetto quelle pescate. Ragionando su questo semplice metodo possiamo facilmente ricavare il numero di sequenze possibili al variare di k.

• Se k = 1 ovviamente ho 26 possibili sequenze di una lettera, una per ciascuna lettera.
• Se k = 2 per la prima lettera pescata avrò 26 possibilità diverse, mentre per la seconda il numero di possibilità si è ridotto a 26-1 = 25 perché la lettera pescata in precedenza non è più ammissibile (e pertanto non è stata rimessa nel sacchetto).

Per trovare il numero delle sequenze ottenibili posso anche utilizzare un metodo grafico che consiste nel disegnare un diagramma ad albero in cui da un punto di partenza fissato faccio partire un numero di rami uguale al numero dei possibili esiti di ciascuna estrazione. Così facendo il numero dei rami nel livello più alto corrisponderà al numero di sequenze possibili. Nel caso k = 1 abbiamo 26 rami che si diramano dal punto di partenza. Nel caso k = 2 aggiungiamo al grafico del caso precedente 25 ulteriori diramazioni per ciascuno dei 26 rami già presenti al primo livello. Il totale dei rami per k = 2 sarà quindi 26*25 = 650.

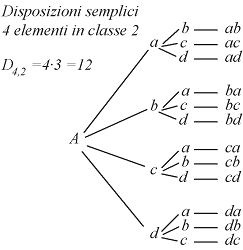
diagramma ad albero delle disposizioni semplici di k = 2 elementi presi in un insieme di n=4 costituito dalle prime 4 lettere dell'alfabeto.

Il nostro ragionamento può essere ripetuto e generalizzato fino a quando il numero di lettere pescate non raggiunge quello delle lettere nel sacchetto, portandoci alla formula:

Ad esempio proviamo a considerare quante sono le sequenze di 4 lettere prive di ripetizioni ottenibili dall'alfabeto internazionale di 26 lettere:

Disposizioni con ripetizione

Sono sequenze ordinate in cui ciascuna lettera può comparire più volte. Il numero di sequenze ottenibili secondo queste regole sarà più elevato del caso precedente per il semplice fatto che ad ogni sorteggio il numero delle lettere stavolta rimarrà invariato (dobbiamo cioè rimettere ogni volta nel sacchetto la lettera pescata). Quindi seguendo il medesimo procedimento visto per le disposizioni semplici avremo che a ogni nuovo livello del nostro diagramma ad albero il numero di rami che si dipartiranno da uno dei precedenti rimane costante. La formula generale per ottenere il numero di disposizioni con ripetizione pertanto diventa:

In questo caso le sequenze di 4 lettere ottenibili dall'alfabeto internazionale di 26 lettere diventano:

Come ben saprete, soprattutto chi di voi ha mai giocato a Scarabeo, nella lingua italiana solo un minuscolo sottoinsieme di tutte le possibili sequenze di 4 lettere hanno un significato, nello specifico solo 1146 sulle 456976 possibili, corrispondenti allo 0,25% del totale. [2]

Permutazioni semplici

Si chiama permutazione di n oggetti distinti ogni ordinamento degli n oggetti dati.

Se considero un mazzo di carte ogni volta che lo mescolo non faccio altro che variare l'ordine iniziale generando così una permutazione. Quante sono le possibili permutazioni di n oggetti distinti come le carte da gioco? La formula coincide con quella già vista per le disposizioni semplici nel caso in cui k = n.

Matematicamente equivale al fattoriale del numero degli n elementi distinti, indicato con il simbolo n!. In un mazzo da poker composto da 52 carte da gioco le permutazioni ottenibili sono:

un numero così alto ci fa capire che mescolando accuratamente un mazzo di carte le probabilità di riottenere lo stesso ordine iniziale sono praticamente nulle.

Permutazioni con ripetizione

Un altro esempio di permutazione ben nota agli appassionati di enigmistica sono gli anagrammi. Data una parola si deve trovarne una seconda variando l'ordine delle lettere che la compongono. Dato che la maggior parte delle parole contengono lettere ripetute possiamo considerare gli anagrammi come un esempio di permutazioni con ripetizione:

Si chiama permutazione con ripetizione ogni permutazione di n oggetti NON tutti distinti tra loro.

il numero di permutazioni con ripetizione è inferiore a quello senza ripetizione perché vanno esclusi dal conteggio quegli scambi tra lettere uguali che non cambiano il significato della sequenza.

MAMMA = MAMMA

per ciascuna delle permutazioni della parola mamma, possiamo costruire 2! permutazioni permutando tra loro le due lettere A. La stessa cosa vale per le tre lettere M ma stavolta per ciascuna permutazione saranno 3! = 6 quelle ottenibili scambiando tra loro le tre M ...

MAMMA = MAMMA = =MAMMA = MAMMA = =MAMMA = MAMMA

Quindi per ottenere il numero di permutazioni con ripetizione il fattoriale del numero di lettere che compongono la parola va diviso per il prodotto dei fattoriali delle permutazioni possibili per le lettere che si ripetono:

Generalizzando possiamo dire che le permutazioni con ripetizione di n oggetti (di cui a₁ uguali tra loro, a₂ uguali tra loro e distinti dai precedenti, ..., a_k uguali tra loro e distinti dai precedenti) con a₁ + a₂ + ... + a_k = n sono date dalla formula:

Combinazioni semplici

Dato un insieme di n elementi, si chiama combinazione semplice degli n elementi di classe k (con k minore o uguale a n) ogni sottoinsieme dell'insieme dato avente k elementi

Il numero complessivo di combinazioni di n oggetti di classe k in matematica è rappresentato da un simbolo specifico, che prende il nome di coefficiente binomiale

definito a condizione che n sia maggiore o uguale a 1 e che 0 ≤ k ≤ n. Riflettiamo su alcuni casi particolari:

dal momento che l'unico sottoinsieme di 0 elementi di qualunque insieme è l'insieme vuoto.

dato che il numero di sottoinsiemi composti da un solo elemento corrisponderà per forza di cose con il numero n di elementi nell'insieme.

Combinazioni con ripetizione

Dati n oggetti distinti, si chiama combinazione con ripetizione degli n oggetti di classe k, ogni raggruppamento non ordinato di k oggetti, scelti tra quelli assegnati, ammettendo la possibilità di ripetere gli oggetti

Il numero di combinazioni con ripetizione di n oggetti di classe k equivale al numero di n-uple di interi non negativi (x_1, ... , x_n) soluzioni dell'equazione:

x_1 +, ... , + x_n = k

ed è assegnato dalla formula:

Esempio

Quanti possibili tipi di confezioni da 10 di M&M's di colore rosso, giallo e verde si possono confezionare?

Ogni possibile confezione può essere rappresentata come un raggruppamento di 10 lettere, scelte tra le iniziali dei 3 diversi colori possibili R = Rosso, G = Giallo, V = Verde. Una confezione contenente 5 confetti rossi, 2 gialli e 3 verdi verrà rappresentata in questo modo:

RRRRRGGVVV

Questo problema equivale a stabilire il numero di combinazioni con ripetizione di n = 3 oggetti di classe k = 10. Dal momento che le lettere/colori possono essere ripetute e che l'ordine non ha importanza una confezione resta univocamente determinata una volta stabiliti i numeri x_rosse , x_verdi , x_gialle che soddisfano l'equazione:

Quindi il nostro problema equivale a quello di stabilire il numero di terne che soddisfano questa equazione. Se rappresento la mia confezione in questo modo:

considerando i confetti come asterischi e mettendo una barra verticale per separare i confetti di colore diverso l'insieme delle terne corrisponde con le permutazioni di n + (k -1) oggetti di cui n uguali tra loro e (k-1) uguali tra loro e distinti dai precedenti.

Bibliografia